Recently, a friend dropped this nugget:

• Between the numbers 0-9, exactly 10% contain the digit "7".
• For 0–99, it's 19%.
• For 0–999, it's 27.1%.
• And for larger ranges, this count approaches 100%.

If you asked me to prove that two odd numbers make an even one, I'd just stare at the floor in shame (and that's despite somehow having crawled out of uni with a math-adjacent degree). But show me something like this and I'll start glowing like radioactive candy. So naturally my brain didn't even stop to think about the math, it just yelled: this needs to be a graph!

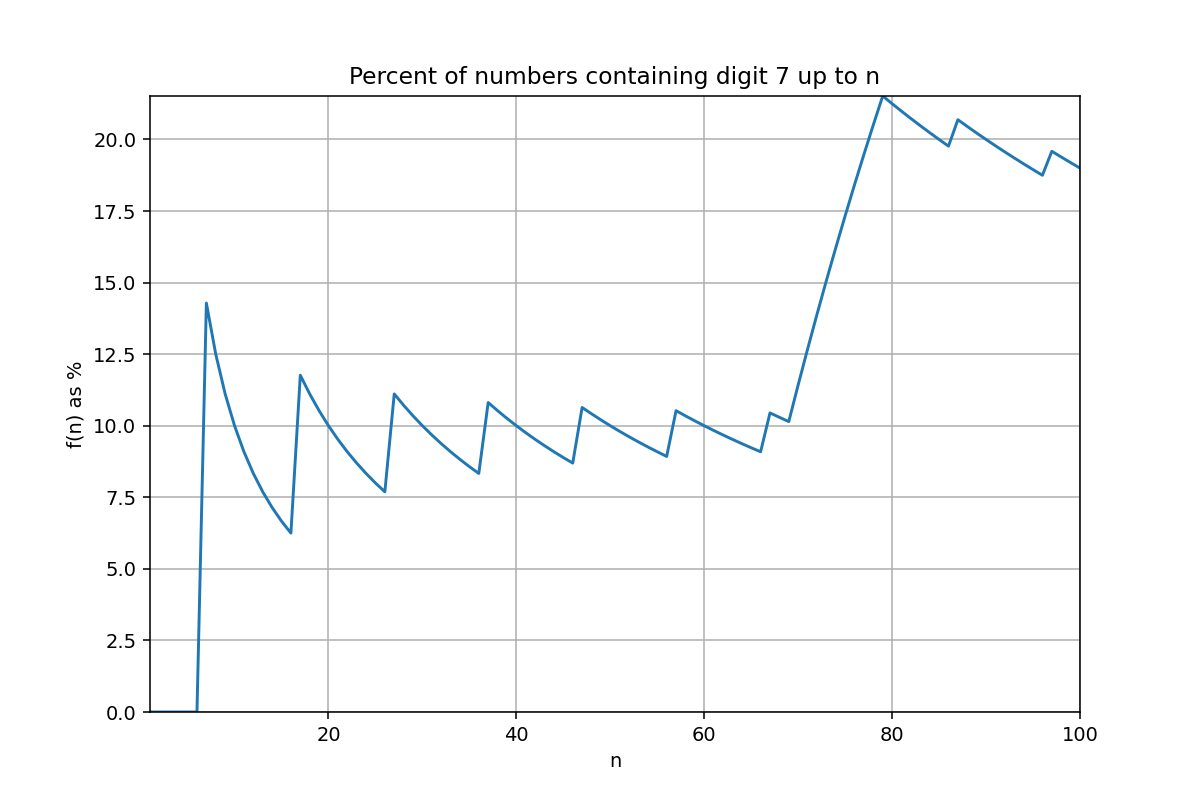
Digit 7

Five minutes later:

I'd been tunneling in coding autopilot, not even thinking, so I half-expected some smooth curve to pop out… and got this jagged little sawtooth instead. How pretty! And once I let my brain clock back in, it's obvious: the share of 7's drifts downward, then twitches upward at every "x7", with a bigger jolt whenever we hit a whole block of "7x". Of course it was never going to be a smooth curve.

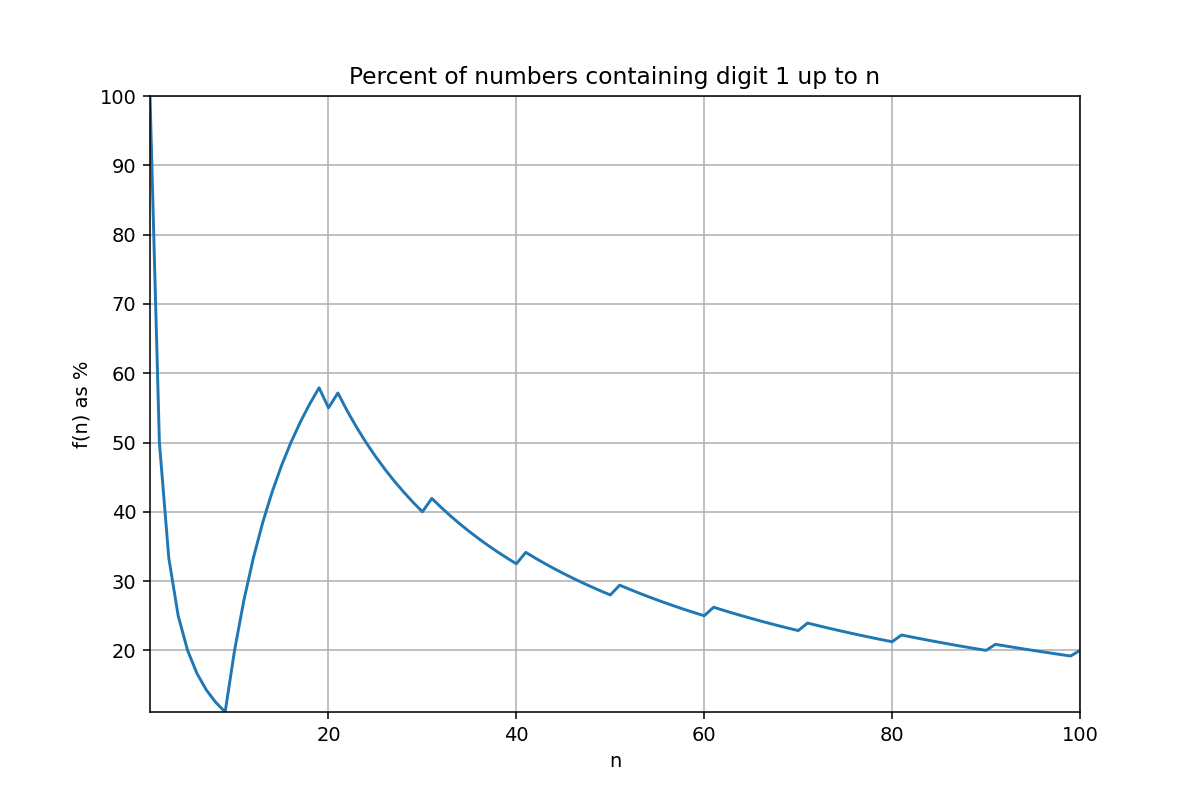
Digit 1

OK, but what if we asked about the digit 1?

Naturally, the big bump happens around 10–19. What's sneakier is the curvature, now more prominent, which comes simply from the fact that f(n) is a ratio:

n	Numbers with "1" from 0..n	f(n)
1	1	1/1 = 100.000%
2	1	1/2 = 50.000%
3	1	1/3 = 33.333%
4	1	1/4 = 25.000%
5	1	1/5 = 20.000%
6	1	1/6 = 16.667%
7	1	1/7 = 14.286%
8	1	1/8 = 12.500%
9	1	1/9 = 11.111%
10	1, 10	2/10 = 20.000%
11	1, 10, 11	3/11 = 27.273%
12	1, 10, 11, 12	4/12 = 33.333%
13	1, 10, 11, 12, 13	5/13 = 38.462%
14	1, 10, 11, 12, 13, 14	6/14 = 42.857%
15	1, 10, 11, 12, 13, 14, 15	7/15 = 46.667%
16	1, 10, 11, 12, 13, 14, 15, 16	8/16 = 50.000%
17	1, 10, 11, 12, 13, 14, 15, 16, 17	9/17 = 52.941%
18	1, 10, 11, 12, 13, 14, 15, 16, 17, 18	10/18 = 55.556%
19	1, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19	11/19 = 57.895%
20	1, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19	11/20 = 55.000%

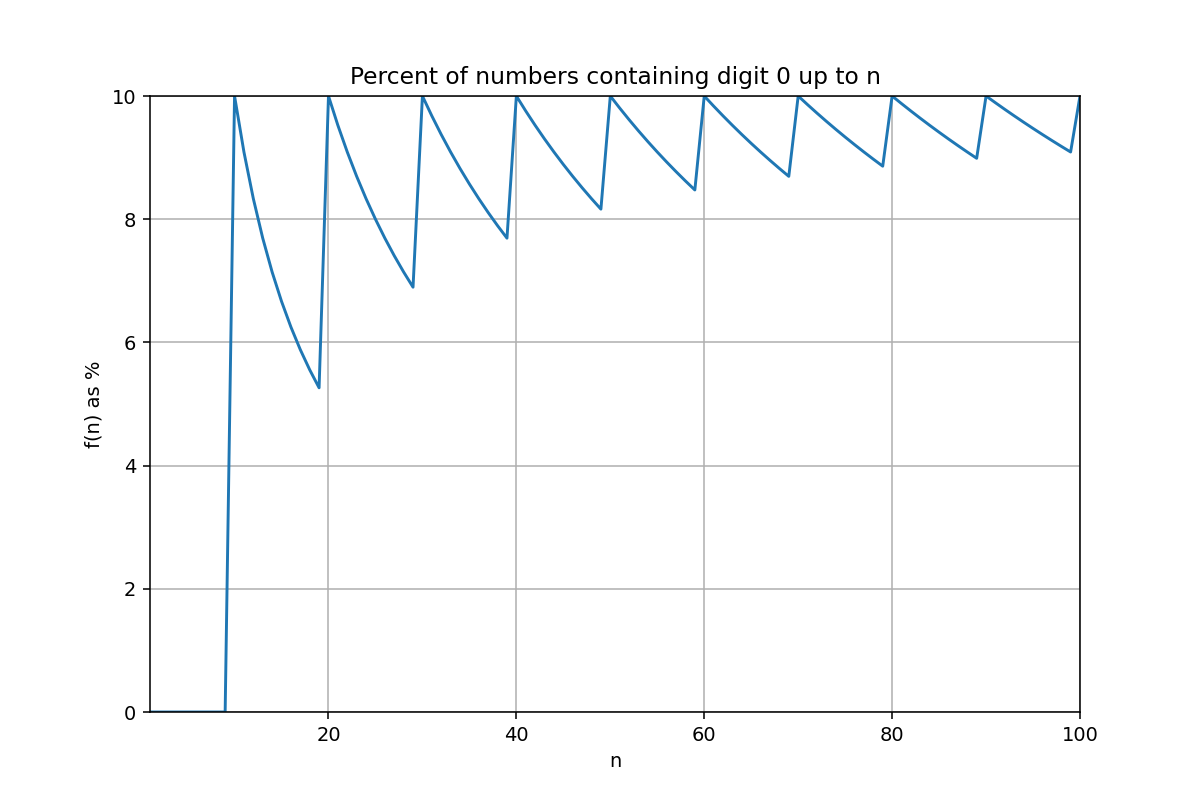
Digit 0

Now what about 0 – is it any special?

Well, a little. No flashy bump early on, because no number starts with 0 (rude). But once you stretch the range, it plays the same game as the others.

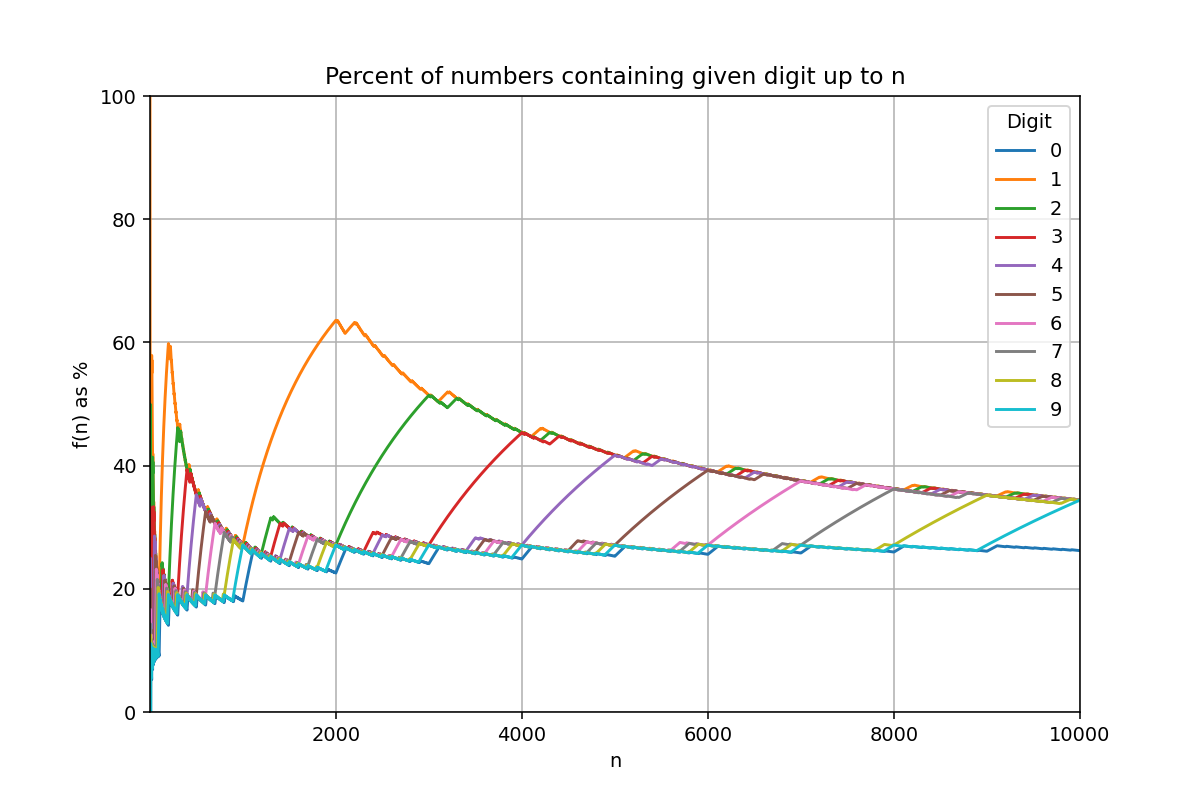
All digits together

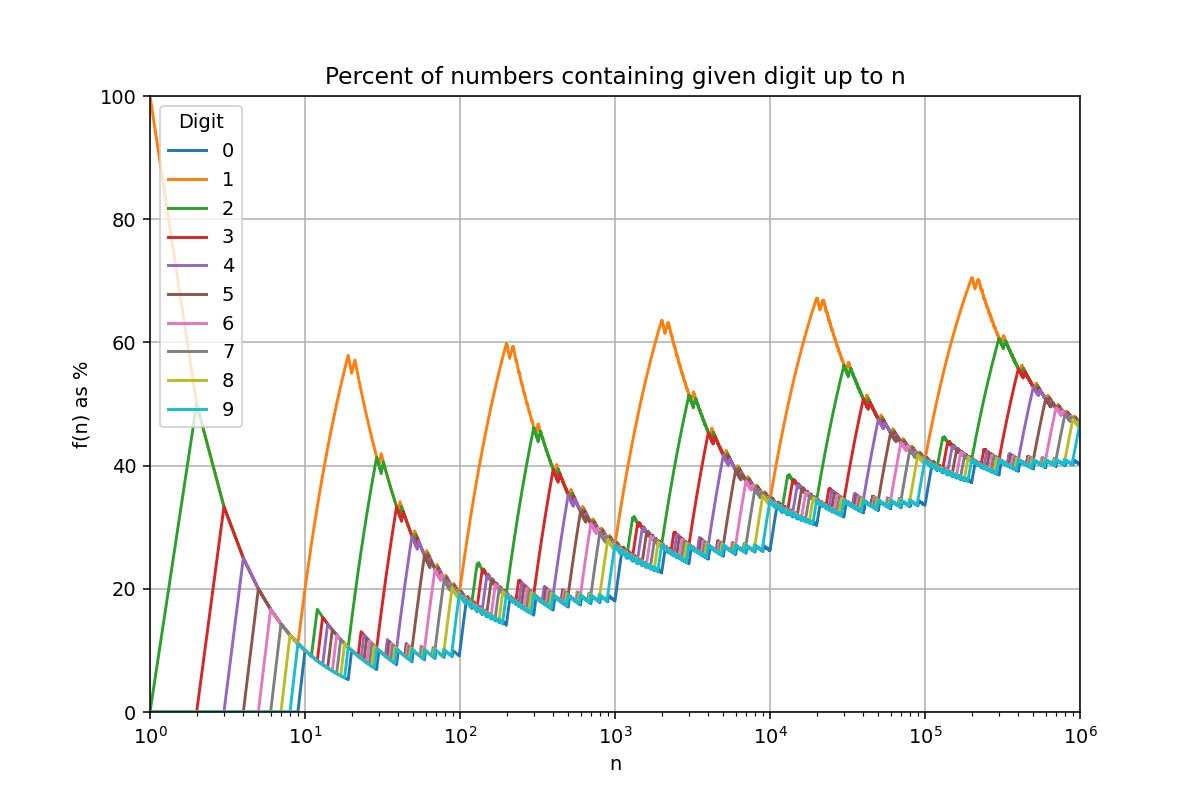
The real eye-candy comes when we plot all digits across a wider range:

Whoa!

My friend called this a sword. Now I can't unsee a Final Fantasy boss fight where the hero pulls out the Graph of Digits as a limit break.

Each digit gets a big spike when its block comes up (1000–1999 for 1, 2000–2999 for 2, and so on), then the percentage slowly drops as more numbers get added and the digit's influence gets diluted. This time, let's try switching to log scale and sample even wider range:

There! Much cleaner. The spikes line up because our number system is literally powers of ten. Each digit gets its fifteen minutes of fame once per decade, then fades until the next cycle. Add more digits, and this drama repeats, only at more cosmic scales.

Also, it goes without saying, but between those highs and lows, the pieces link together into little curves of their own, making the whole thing self-similar. Is it officially a fractal? Does it have a Hausdorff dimension? I told you, I've no clue.

But damn, it looks rad.

Appendix: here's the Python script I used to make the images, in case you want to check another base, improve my DP, or just redraw the same spikes.

#!/usr/bin/env python3
import matplotlib.pyplot as plt


def make_plot(filename, digits, N, log_scale=False, _cache={}):
    x = range(1, N + 1)
    w = 1200
    h = 800
    dpi = 140
    plt.figure(figsize=(w / dpi, h / dpi))
    if log_scale:
        plt.xscale("log")
    plt.margins(0)
    plt.xlabel("n")
    plt.ylabel("f(n) as %")
    plt.title(
        f"Percent of numbers containing digit {digits[0]} up to n"
        if len(digits) == 1
        else f"Percent of numbers containing given digit up to n"
    )

    # cache builder
    for d in digits:
        if d not in _cache or len(_cache[d]) <= N:
            start = len(_cache.get(d, []))
            counts = _cache.get(d, [0])
            for i in range(start, N + 1):
                counts.append(counts[-1] + (str(d) in str(i)))
            _cache[d] = counts

        y = [_cache[d][i] * 100 / i for i in x]
        plt.plot(x, y, label=str(d))

    if len(digits) > 1:
        plt.legend(title="Digit")
    plt.grid(True)
    plt.savefig(filename, dpi=dpi)
    plt.close()


make_plot("plot_1.png", [7], 100)
make_plot("plot_2.png", [1], 100)
make_plot("plot_3.png", [0], 100)
make_plot("plot_4.png", list(range(10)), 10000)
make_plot("plot_5.png", list(range(10)), 1_000_000, log_scale=True)